Dalton's Dev Blog

插值那些事——译Interpolation Tricks

 2130  5 分钟

引言

插值这个概念是在几年前看到的，当时不是很理解，以为是一个数学概念就忽略了，实际上这个东西应用很多，特别是在游戏开发中，我们要做实时渲染，如果说只有0和1，中间没有过渡的话，一切都会显得很生硬，下面这篇文章是我看到的最好的解释这个概念及其应用的文章，传送门地址。

插值技巧

或者说我如何做到停止烦恼并爱上0~1区间的

  1. 为什么是0…1这个范围

当在做游戏原型时我发现了许多不同的插值技巧，这些非常有价值，比如在各种移动中增加一些平滑，这些移动可以是摄像机，物体，灯光渐隐渐现等等，你会发现增加这些技巧之后会更加的令人享受。生硬的移动会让人觉得不舒服，应该极力避免。

一般说来，当做一些动画时，我们都会知道一个起始位置和终止位置，然后在他们中间可以进行一些过渡，所有的这些都可以转化为0到1的问题。（其实随机数也是类似的道理）

0值还有1值有很多有趣的属性，基于这些属性你可以拼接出任意开始和结束的值，正因为如此，所以我们只要把0到1的过程处理掉即可。

  1. 开始进入0到1区间

如果我们希望将一个变量X从A移动到B点，通过N步，那我们应该写如下代码

1
2
3

for (i = 0; i < N; i++) {
	X = ((B * i) + (A * (N - i))) / N;
}

或者我们重新写一下

1
2
3
4

for (i = 0; i < N; i++) {
	t = i / N;
	X = (B * t) + (A * (1 - t));
}

这样看起来清楚多了吧？此时t的范围从0到1。

  1. 线性插值（Linear Interpolation）

用N个离散步数从0移动到1被称为线性插值，或者叫“lerp”，见下图

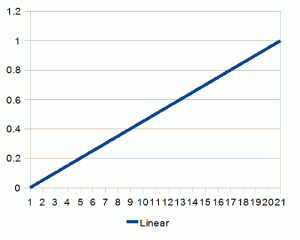
linear-300x240

linear.swf

依靠线性插值可以解决很多从A到B的基本问题，但是如果从B点重新运动回A点，也是通过同样的线性插值，你就会发现有明显的不和谐。幸运的是，这里不仅仅有一种方案能够解决从A到B的问题（实际上有无数种，但我们将只关注一部分）。

  1. 更平滑的步骤（smoothstep）

如果你从这个小教程中带不走其他的，那就带走它

1

#define SMOOTHSTEP(x) ((x) * (x) * (3 - 2 * (x)))

smoothsetp就好像一种神奇的盐，你可以把它洒在任何你想变得更好的地方，你可以很简单的替换大多数的线性插值，如下

1
2
3
4
5

for (i = 0; i < N; i++) {
	t = i / N;
	t = SMOOTHSTEP(t);
	X = (B * t) + (A * (1 - t));
}

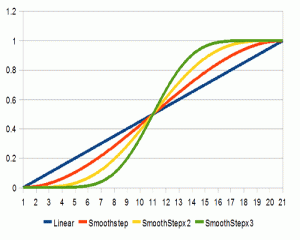
smoothstep看起来是这样的

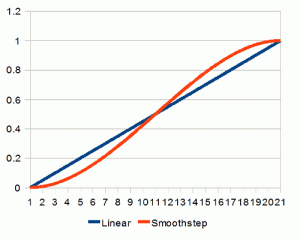
smoothstep-300x240

smoothstep.swf

通过对比，你可以很明显的看到他刚开始会加速，当快要接触目标的时候会慢慢减速。

  1. 高次幂（higher powers） 如果你只想要有缓慢的加速时间，简单的加个N次幂可以解决问题，如下
1
2
3
4
5

for (i = 0; i < N; i++) {
	t = i / N;
	t = t * t;
	X = (B * t) + (A * (1 - t));
}

如果你更想要的是缓慢减速，上面的式子做下反相就行了

1
2
3
4
5

for (i = 0; i < N; i++) {
	t = i / N;
	t = 1 - (1 - t) * (1 - t);
	X = (B * t) + (A * (1 - t));
}

两个式子看起来是这个样子的

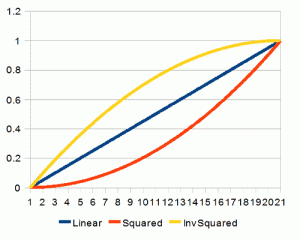
squared-300x240

squared.swf

如果我们把次幂再调高到立方次，这个曲线看起来是这样的

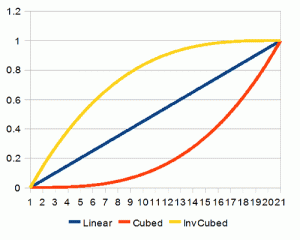
cubed-300x240

cubed.swf

同样的道理，这个还可以再次应用smoothstep，应用smoothstep到已经被平滑过的值可以让曲线更进一步（真不知道怎么翻），这个结果不是很容易应用到所有东西上，正如你所见，他会在原地待一段时间，但是有时候又很有用（也不说什么时候有用）。

smoothstepx-300x240

smoothstepx.swf

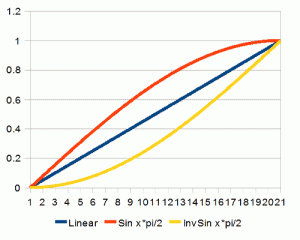
  1. 正弦

另外一个方便的曲线就是正弦，正弦可以像幂函数一样应用，结果也是十分相似的。

1
2
3
4
5

for (i = 0; i < N; i++) {
	t = i / N;
	t = sin(t * Pi / 2);
	X = (B * t) + (A * (1 - t));
}

这个曲线同样可以像幂函数一样反相，结果如下

sin-300x240

sin.swf

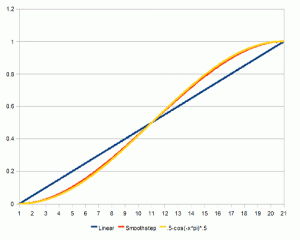
如果我们使用了整条三角函数，我们可以可以将曲线做得很近似于smoothstep

cos-300x240

cos.swf

1
2
3
4
5

for (i = 0; i < N; i++) {
	t = i / N;
	t = 0.5 - cos(-t * Pi) * 0.5;
	X = (B * t) + (A * (1 - t));
}

不过，使用三角函数会比刚才的方法有更大的开销。

  1. 加权平均（weighted average）

一个相当方便的算法，特别是当你没办法知道未来的目标行为时（比如摄像机跟随者角色，目标点点一直在改变）。注，这种算法应用很多，你甚至都不需要记录当前时间t，所以特别方便。

1

t = ((t * (N - 1)) + w) / N;

其实我更喜欢这么写（这段是我自己拼的）

1

t += ((w - t) / N;

是的，当t越靠近w，则累加量越少。 t代表当前值，w代表目标点，N是缓动因子，N值越大，t接近w就越慢。

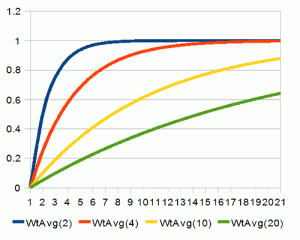
wtavg-300x240

wtavg.swf

t越靠近w，则他运动得就越慢，越远离，他就越快，在理想的世界中，t实际上将永远到不了w，只是他们之间的距离越来越小越来越小，再说，计算机是不理想的。

  1. 样条

最后，如果你需要更多的控制，你可以使用样条，Catmull-Rom样条是一个非常方便的方法，他总是会经过控制点，所以他可以更容易的应用到插值计算中，而其他的样条函数可以得到更自然的曲线，但是也有更少的可预知性，这里有份实现Catmull-Rom函数的代码。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

float catmullrom(float t, float p0,  float p1, float p2, float p3) {
	return 0.5f * (
	(2 * p1) +
	(-p0 + p2) * t +
	(2 * p0 - 5 * p1 + 4 * p2 - p3) * t * t +
	(-p0 + 3 * p1 - 3 * p2 + p3) * t * t * t
	);
}

for (i = 0; i < N; i++) {
	t = i / N;
	t = catmullrom(t, Q, 0, 1, T);
	X = (B * t) + (A * (1 - t));
}

在正常使用中，你可以给他很多的控制点，比如，5， 6， 比如4， 7，你能做出很多不一样的效果，下面就是一些例子。

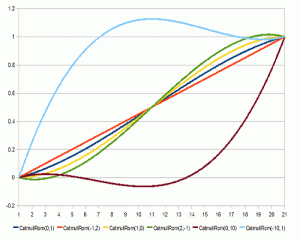
catmullrom-300x240

splines.swf

上面的参数值是Q和T的值，即p0, p3。 注意：这个值必须经过0和1，但是并不意味着要在0和1之间。

  1. 结论

我希望这个简短的技术概览教程可以帮助你从你的移动行为中去掉那些尖锐的角落。

更多的阅读

updatedupdated2021-01-202021-01-20